KNN算法及利用KNN检测异常操作
文章最后更新时间为:2019年01月01日 18:26:03
1 KNN算法
1.1 KNN简介
K近邻算法的核心思想可以用一句很多文化中都有的古语概括:近朱者赤近墨者黑。评价一个人,一般从它的朋友就可以得知,因为一般和小混混整天呆在一起的就是小混混,和小学生一起玩的一般也是个小学生。KNN的基本思路也是这样,如果一个待分类的样本在样本空间中的K个最相近的样本中的大多数属于某个类别,那么该样本也属于这个类别。
KNN直接作用于带标记的样本,属于有监督的算法。
1.2 距离度量
KNN算法做分类任务时,需要对样本的相似度进行判断。“距离”和“相似系数”就是对相似度的两种度量方式,它是机器学习的核心概念之一,这里介绍一下几个常用的距离计算方式。
1.2.1 欧式距离
欧式距离源于两点间的距离公式,指M维空间中两个点的真实距离。
两个n维向量P1(X11,X12,X13,……,X1n)和P2(X21,X22,X23,……,X2n)之间的欧式距离为:
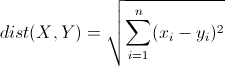
计算(1,2)和(4,6)的欧式距离:
>>> import numpy as np
>>> from math import *
>>> x = np.array([1,2])
>>> y = np.array([4,6])
>>> sqrt(sum(pow(x-y,2) for x,y in zip(x,y)))
5.01.2.2 曼哈顿距离
曼哈顿距离也就是欧几里得空间的固定直角坐标系两点形成的线段对轴产生的投影的距离的总和。想象你在曼哈顿要从一个十字路口开车到另一个十字路口,驾驶距离是两点之间的直线距离吗?显然不是。
两个n维向量P1(x11,x12,…,x1n)与P2(x21,x22,…,x2n)间的曼哈顿距离为:

计算(1,2)和(4,6)的曼哈顿距离:
>>> sum(abs(x-y))
71.2.3 切比雪夫距离
国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是max(|x2-x1|,|y2-y1|) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。
两个n维向量P1(x11,x12,…,x1n)与P2(x21,x22,…,x2n)间的切比雪夫距离:
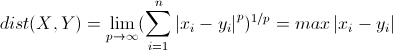
计算(1,2)和(4,6)的曼哈顿距离:
>>> abs(x-y).max()
41.2.4 夹角余弦距离
夹角余弦距离是用向量空间中的两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。向量,是多维空间中有方向的线段,如果两个向量的方向一致,即夹角等于0,那么这两个向量相近。
对于两个n维样本点P1(x11,x12,…,x1n)和P2(x21,x22,…,x2n),它们之间的夹角余弦距离为:
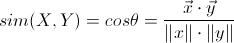
计算(1,2)和(4,6)的曼哈顿距离:
>>> np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))
0.99227787671366771.3算法过程
- 1 计算距离:给出待分类的样本,计算样本和其他样本的距离
- 2 距离排序:将计算出的距离排序
- 3 选择k个相邻:找出k个距离最近的样本
- 3 决定分类:找出k个距离最近样本的主要分类,作为此待分类样本的类别
1.4 要素
KNN算法的分类结果由3个基本要素组成:距离度量、K的选择和分类决策。
2 利用KNN算法检测异常操作
黑客入侵Web服务器以后,通常会通过系统漏洞进一步提权,获得root权限。我们试图通过搜集Linux服务器的bash操作日志,来检测其中是否存在非正常可疑操作。
2.1 数据搜集
Schonlau在他的个人网站:http://www.schonlau.net/上发布了针对Linux操作的训练数据。我们直接下载即可。
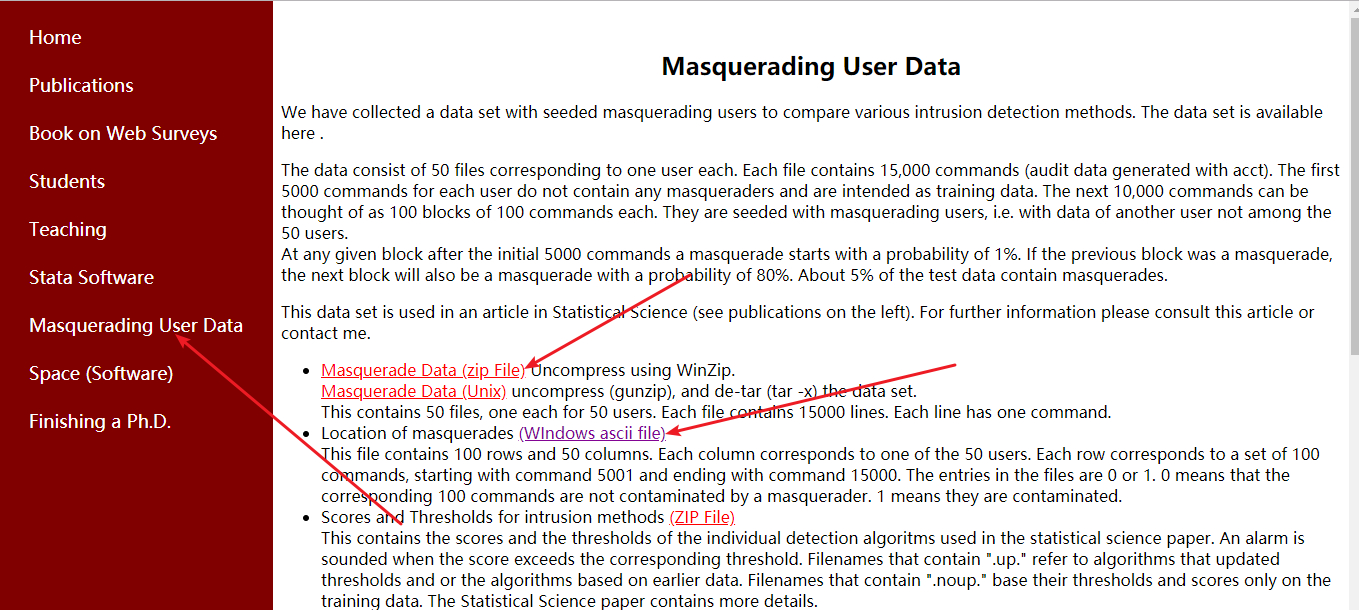
训练数据包含50个用户的操作日志(网站上对应红框处“Masquerade Data(zip File)”)和一个标签文件label.txt(网站上对应的红框处“WIndows ascii file”)
每个用户命令为15000条,前5000条是正常数据,后10000条随机包含了异常操作。其前5000条都分类成正常即可,因此laber.txt也就默认没有这部分,只对后10000条打了标签。将每100个操作分为一组,这样也就是150组操作。只要一组操作中出现了一个异常操作,就认为这组操作是异常的。
2.2 数据特征化
这里只用到一个用户的操作就好,我们选择user3即可,我们首先将150组操作分为120组训练样本和30组待检测样本。
样本我们有了,但是每个样本是100个命令组成的列表。这样怎么计算其相似度呢?这里我们将其标量化,具体做法是:
- 第一步:对日志中所有操作命令使用次数进行排序,选出使用最多的前50条记做M1,选出使用最少的前50条记做M2。
- 第二步:每100条操作命令组成一个操作序列,这样的序列有150个,这100条操作中不重复的命令个数,记做F1。100条操作中最多的10条且在M1中的命令个数(重合度),记做F2 。这100条操作中最少的10条且在M2知乎的命令个数(重合度),记做F3 。一个序列{F1,F2,F3}就作为这个序列的特征,这样的特征有150个,前面120个作为训练集,后面30个作为测试集。
- 第三步:打标签,前50个正常全部是0,后100个有0也有1。后100条从lable.txt中读取,user3就对应第三列
特征化的代码如下:
import operator
from nltk import FreqDist
def load_user_cmd(filename):
cmd_list=[]
dist=[]
with open(filename) as f:
i=0
x=[]
for line in f:
line=line.strip('\n')
x.append(line)
dist.append(line)
i+=1
if i == 100:
cmd_list.append(x)
x=[]
i=0
fdist = sorted(FreqDist(dist).items(),key = operator.itemgetter(1),reverse = True)
dist_max = [item[0] for item in fdist[:50]]
dist_min = fdist[-50:]
return cmd_list,dist_max,dist_min
# cmd_list包含150组数据,每组100个命令,所以一共是15000个命令。
# dist_max 最常用的50个命令
# dist_min 最不常用的50个命令
def get_user_cmd_feature(user_cmd_list,dist_max,dist_min):
user_cmd_feature = []
for cmd_block in user_cmd_list:
f1 = len(set(cmd_block))
fdist = sorted(FreqDist(cmd_block).items(),key = operator.itemgetter(1),reverse = True)
f2=fdist[0:10]
f3=fdist[-10:]
f2 = len(set(f2) & set(dist_max))
f3=len(set(f3) & set(dist_min))
x=[f1,f2,f3]
user_cmd_feature.append(x)
return user_cmd_feature
def get_label(filename, index = 0):
x=[]
with open(filename) as f:
for line in f:
line=line.strip('\n')
x.append(int(line.split()[index]))
return x
if __name__ =="__main__":
user_cmd_list,user_cmd_dist_max,user_cmd_dist_min = load_user_cmd("../masquerade-data/User3")
user_cmd_feature = get_user_cmd_feature(user_cmd_list,user_cmd_dist_max,user_cmd_dist_min)
labels = get_label("../masquerade-data/label.txt",2)
y = [0]*50+labels
N = 120
x_train=user_cmd_feature[0:N]
y_train=y[0:N]
x_test=user_cmd_feature[N:150]
x_test=y[N:150]2.3 KNN训练
我们已经得到了x_train、y_train、x_test、x_test。接下来调用sklearn的KNeighborsClassifier直接训练。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
if __name__ =="__main__":
knn = KNeighborsClassifier(n_neighbors=3) # 创建分类器,这里algorithm采用'auto',会在学习时自动选择最合适的算法
knn.fit(x_train,y_train) # 训练
predictions = knn.predict(x_test) # 测试
print(accuracy_score(y_test, predictions)) # 验证最终结果是100%,当我们改变N的取值,也就是样本集和测试集的大小改为80和70时,得分来到了83%。因为样本中标签为1的很少,所以这种结果不是很理想,总感觉特征化的过程有点突兀,莫名其妙。
查看得知预测的结果都是0,而用于测试的数据其标签0多,1少,所以导致后续的结果看起来正确率很高。
2.3 改进
刚才特征化的时候只比较了最频繁和最不频繁的操作命令,事实上特征效果不太明显。这次我们尝试进行全量比较,首先将全部命令去重后形成一个大型向量空间。
def load_user_cmd_new(filename):
cmd_list=[]
dist=[]
with open(filename) as f:
i=0
x=[]
for line in f:
line=line.strip('\n')
x.append(line)
dist.append(line)
i+=1
if i == 100:
cmd_list.append(x)
x=[]
i=0
fdist = list(FreqDist(dist).keys())
# fdist 去重后的全部命令列表
# cmd_list包含150组数据,每组100个命令,所以一共是15000个命令。
return cmd_list,fdist
user_cmd_list,dist = load_user_cmd_new("../masquerade-data/User3")然后使用词集将操作命令向量化,这个特征化的过程如下,就不解释了,看代码很容易理解。
def get_user_cmd_feature_new(user_cmd_list,dist):
user_cmd_feature=[]
for cmd_list in user_cmd_list:
v=[0]*len(dist)
for i in range(0,len(dist)):
if dist[i] in cmd_list:
v[i]+=1
user_cmd_feature.append(v)
return user_cmd_feature
user_cmd_feature = get_user_cmd_feature_new(user_cmd_list,dist)然后训练模型和验证:
labels = get_label("../masquerade-data/label.txt",2)
y = [0]*50+labels
N = 100
x_train=user_cmd_feature[0:N]
y_train=y[0:N]
x_test=user_cmd_feature[N:150]
y_test=y[N:150]
knn = KNeighborsClassifier(n_neighbors = 3) # 创建分类器
knn.fit(x_train,y_train) # 训练
predictions = knn.predict(x_test) # 测试
print(predictions)结果是100%,多次改变N的大小和输出predictions,发现predictions总为0。虽然特征化的过程改进了,但是由于数据集的1出现概率很低导致KNN算法不太实用,总之我个人觉得不太可行。
3 参考
- 《python机器学习实战》
- 《web安全机器学习入门》