[编译原理] 简易计算式的翻译程序设计
文章最后更新时间为:2019年01月16日 13:55:21
这篇文章记录一下最近写的编译原理实习,因为时间紧急(拖延),所以没有实现本来计划的C语言翻译程序,只是实现了计算式的翻译。用的是python语言 (如果时间足够还是用lex和yacc专业工具比较好)。
先来看一下结果:

输入一个计算式,如1+9-19/2+32输出中间代码四元式。
1 词法分析
词法分析最简单了,直接遍历输入的字符串:
- 遇到关键字(+-*/)就直接将关键字提取出来
- 遇到数字就继续看下一个字符,直到不是数字,然后将数字串提取出来
- 遇到下划线或者字母,也继续向后看,提取出变量
上述词法分析将数字或者变量都归类为id,本质上无差别
程序的逻辑如下所示
_content = "" # 这是输入的字符串
# 首先定义一下关键字
_keywords = {"+":"+", '-':"-", '*':"*", "/":"/", "(":"(", ")":")" }
_alphabet = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
_digit = ['0','1','2','3','4','5','6','7','8','9']
def lexical_analysis():
global _content, _p
_p += 1
token = []
value = _content[_p] # 取第一个字符
while value == " ": # 如果是空格,跳过,直到是有效字符
_p += 1
value = _content[_p]
if value in _keywords.keys(): # 如果是关键字,则直接返回token
token.append(_keywords[value])
token.append(value)
return token
elif value in _digit and value != '.': # 如果是数字,则一直接收下一个,直到不是数字为止
num= ''
while value in _digit or value == '.':
num = num + value
_p += 1
try:
value = _content[_p]
except:
break
_p -= 1
# 因为数字中直接加入了小数点,所以这里还得判断有几个小数点,多了就报错,比如10.1.1
if num.count('.') == 0 or num.count('.') == 1 and num[-1:] != '.':
token.append("id")
token.append(num)
return token
else:
print("ID error in" + num)
sys.exit()
elif value.lower() in _alphabet or value == '_': # 遇到字母或者下划线,说明为变量
num = ''
while value.lower() in _alphabet or value in _digit or value == "_":# 一直读下去
num = num + value
_p += 1
try:
value = _content[_p]
except:
break
_p -= 1
token.append("id")
token.append(num)
return token
else:
print("error can not Identification "+value)
sys.exit()
# 这里是主程序:11+(11-10*10)
if __name__ == "__main__":
_content = input("input expression:")
print("----词法分析开始符----")
w = list()
while _p < len(_content)-1:
token = lexical_analysis() # ["ADD","+"]
w.append("< " + token[0] + " , " + token[1] + " >")
print("< " + token[0] + " , " + token[1] + " >")
w.append("< # , # >") # 最后加上结束符
with open("lexical_analysis.txt",'w') as f: # 将结果保存在文本中
for i in w:
f.write(i+'\n')
print("----词法分析结束符----")2 语法分析
词法分析的程序结束了,我们可以得到类似下图的token集合:
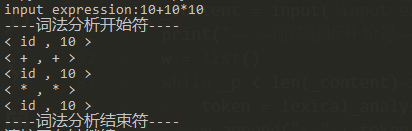
语法分析有很多种方法,这里采用的是LL1分析法,首先构造产生式:
expression => expression + term | expression - term | term
term => term * factor | term / factor | factor
factor => (expression) | - factor | id产生式存在左递归,得消除左递归,使其变成LL1文法:
expression => term expression'
expression' => + term expression' | - term expression' | epsilon(空)
term => factor term'
term' => * factor term' | / factor term' | epsilon(空)
factor => (expression) | - factor | id然后计算出first集和follow集(简写了非终结符号):
计算first集:
FIRST(E) = {-, id, (}
FIRST(E') ={+, -, epsilon}
FIRST(T) = {-, id, (}
FIRST(T') = {*, /, epsilon}
FIRST(F) = {-, id, (}
计算follow集:
FOLLOW(E) = {#, )}
FOLLOW(E') ={#, )}
FOLLOW(T) = {#, ), +, -}
FOLLOW(T') = {#, ), +, -}
FOLLOW(F) = {#, ), +, -, *, /}语法分析采用的是非递归方法,所以需要构造LL1分析表,这里直接利用字典得数据结构来表示:
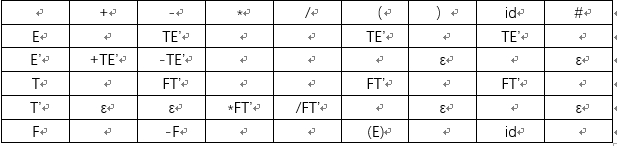
# 创建预测表:
_predict = {
"E":{
"id":["T","E'"],
"(":["T","E'"],
"-":["T","E'"]
},
"E'":{
")":["epsilon"],
"+":["+","T","E'"],
"-":["-","T","E'"],
"#":["epsilon"]
},
"T":{
"id":["F","T'"],
"(":["F","T'"],
"-":["F","T'"]
},
"T'":{
")":["epsilon"],
"-":["epsilon"],
"+":["epsilon"],
"*":["*","F","T'"],
"/":["/","F","T'"],
"#":["epsilon"]
},
"F":{
"id":["id"],
"(":["(","E",")"],
"-":["-","F"]
}
}然后就很简单了,基于分析表驱动即可,程序的逻辑如下:
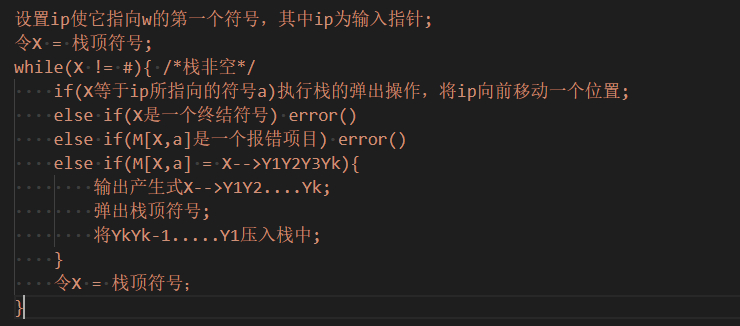
具体实现如下:
def gramma_analysis(w):
mat = "轮数{:<5}已匹配{:<20}\t栈 {:<20}\t输入 {:<20}\t动作{:<20}"
print(mat.format(" "," "," "," "," ",))
stack = list() # 创建符号栈
stack.append("#") # 压入结束符号
stack.append("E") # 压入开始符号E
top = len(stack) - 1 # 栈指针
ip = 0 # 用于记录输入序列w中的终结符的下标,从首部开始
step = 1 # 记录步骤
out_match = '' # 已匹配的字符串
out_stack = '#E' # 输出栈,初始为#E
while stack:
out_input = '' # 记录输入符号串
out_action = '' # 记录执行的动作
a = w[ip].split(' ')[1] # a 用于获取到当前输入符号w[ip] = < id , 11 > ---> a = id
X = stack[top] # X 用于获取栈顶的元素
if X in _T: # 如果栈顶元素为终结符号,判断是否匹配
if X == a: # 如果匹配到终结符
if X == '#': # 如果是最后一个
print("正确结束")
break
else: # 栈弹出,ip前移
out_match = out_match + X # 修改已匹配
stack.pop() # 弹出栈顶元素
top -= 1 # 指针移位
ip += 1 # 指向下一个字符
out_action = "匹配: " + X
else: # 不匹配
print("出错!栈顶终结符不匹配。")
sys.exit()
else: #如果栈顶元素为非终结符,查表展开产生式
if a not in list(_predict[X].keys()):# 如果这个时候M[X,a]是一个报错项目
print("出错!产生式不匹配。")
sys.exit()
else:
stack.pop()
top -= 1
result = _predict[X][a] #得到产生式的右侧,字符串
out_action = "输出: " + X + '-->'
for i in result:
out_action = out_action + i
if result == ["epsilon"]: # Y1Y2...Yk为空
pass
else:
for j in range(len(result)-1,-1,-1):
stack.append(result[j])
top += 1
for i in range(ip,len(w)):
out_input= out_input + w[i].split(' ')[1]
mat = "{:<3}\t {:<15}\t {:<15}\t {:<15}\t{:<15}"
print(mat.format (step, out_match, out_stack, out_input, out_action))
out_stack = "".join(stack)
step += 1输出结果:
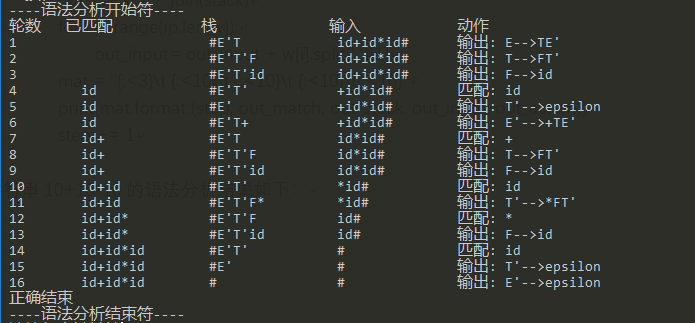
3 语义分析
语义分析只要在语法分析后面加上相应的动作即可,但是思考了很久都没有想明白怎么在LL1非递归中加语义动作,google了一下,大家都是使用递归子程序的方法来实现的,于是只好又写了递归子程序的语法分析,然后在每个子程序中添加动作。
实现逻辑如下:

实现代码如下:
class semantic_analysis:
def __init__(self,w):
self.siyuan = [] # 存放结果
self.table = [] # 词法分析中的后面内容
self.w = w # 词法分析的结果
for i in w:
self.table.append(i.split(' ')[3])
#print(self.w) #['< id , 10 >', '< + , + >', '< id , 10 >', '< * , * >', '< id , 10 >', '< # , # >']
#print(self.table) #['10', '+', '10', '*', '10', '#']
self.ip = 0 # table指针
self.temp_var_count = 0 # 记录临时变量的T数目
self.E()
self.siyuan.append('(='+ ',T'+str(self.temp_var_count) +',0,out)')
for i in self.siyuan: #输出四元式结果
print(i)
def E(self): # E程序 E-->TE'
ret1=self.T()
ret2,ret3 = self.E1()
if(ret2!='epsilon'): #若ret2不为空,则可以产生四元式,否则将变量传递给父项
self.temp_var_count += 1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return 'T'+str(self.temp_var_count)
else:
return ret1
def E1(self): # E'程序 E'-->+TE' | -TE' | epsilon
if(self.table[self.ip]=='+'):
self.ip += 1
ret1=self.T()
ret2,ret3=self.E1()
if(ret2=='epsilon'):
return '+',ret1
else:
self.temp_var_count+=1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return '+','T'+str(self.temp_var_count)
elif(self.table[self.ip]=='-'):
self.ip += 1
ret1=self.T()
ret2,ret3=self.E1()
if(ret2=='epsilon'):
return '-',ret1
else:
self.temp_var_count+=1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return '-','T'+str(self.temp_var_count)
else:
return 'epsilon','epsilon'
def T(self): # T程序
ret1=self.F()
ret2,ret3=self.T1()
if(ret2!='epsilon'):
self.temp_var_count+=1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return 'T'+str(self.temp_var_count)
else:
return ret1
def T1(self): # T1程序
if(self.table[self.ip]=='*'):
self.ip += 1
ret1=self.F()
ret2,ret3=self.T1()
if(ret2=='epsilon'):
return '*', ret1
else:
self.temp_var_count += 1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return '*','T'+str(self.temp_var_count)
elif(self.table[self.ip]=='/'):
self.ip += 1
ret1=self.F()
ret2,ret3=self.T1()
if(ret2=='epsilon'): # 若ret2不为空,则可以产生四元式,否则将变量传递给父项
return '/',ret1
else:
self.temp_var_count+=1
self.siyuan.append('('+ret2+','+ret1+','+ret3+',T'+str(self.temp_var_count)+')')
return '/','T'+str(self.temp_var_count)
else:
return 'epsilon','epsilon'
def F(self): # F程序
if(self.table[self.ip])=='(':
self.ip += 1
ret1=self.E()
self.ip += 1
return str(ret1)
elif(self.table[self.ip] == "-"): # 当为标识符时,传递给父项
self.ip += 1
ret1 = self.F()
self.temp_var_count+=1
self.siyuan.append('( NET' +','+ret1+','+ ',T'+str(self.temp_var_count)+')')
return 'T'+str(self.temp_var_count)
else:
ret1 = self.table[self.ip]
self.ip += 1
return str(ret1)结果:
