python实现RSA算法

9029
密码学
RSA

文章最后更新时间为：2018年12月26日 23:07:29

RSA是一种公钥密码算法，其影响力我就不多说了，算法原理网上多的是，看了几篇，还是觉得阮一峰写的好懂。

可阅读下面文章来了解RSA算法。
RSA算法原理（一）
RSA算法原理（二）

要想实现RSA，其关键在于大数运算，无论是大数之间的加减乘除还是模幂运算，都是普通的数据结构无法完成的，如果你是使用C语言来实现，那么你还需要首先解决五百位数字的加减乘除问题。

但是python语言有个好处，就是自动实现大数运算，其数据结构是不限制位数的。比如

>>> x = 99999999999999999999999999999999999999999999999999
>>> x += 1
>>> x
100000000000000000000000000000000000000000000000000
 
>>> print(999**999)
36806348825922326789470084006052186583833823203735320465595962143702560930047223153010387361450517521869134525758989639113039318944796977164583238219236607653663113200177617597793217865870366077846576581183082787698201412402294867197567813172495806442794

但是如果用C语言就需要自己造轮子，手动构造函数实现大数运算。

没有大数运算的麻烦，实现RSA就简单的多了。现在思考一下，我们还有两个问题。

  • 怎么产生一个大素数
  • 怎么实现大数的模幂运算

接下来我们就来一一解决这两个问题。

1.实现大数的模幂运算

为什么先解决这个呢，因为大素数的产生需要用到这个函数，所以我们首先实现大数的模幂运算。

先来考虑一个简单的问题，怎么计算 3 ^ 13 (mod 9)？

那还用想？直接用计算机算 3 ^ 13 不就好了，但是如果是33333 ^ 1333333333呢，这计算机得算到什么时候，所以我们得想个法子减少计算量。

这里要利用到我们所熟知的两个公式

(a * b) (mod n) = a (mod n) * b (mod n)

a ^ (b+c) = a^b * a^c

那么上面的13 = 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0。3^13就可以转化为3^(1*2^3) * 3^(1*2^2) * 3^(0*2^1) * 3^(1*2^0)

到这里我们就清楚了。我们可以先算3^(1*2^0) (mod 9)，假设其结果为res。然后再算3^(0*2^1) (mod 9), 那么这个就等于0 * res^2 (mod 9)，所以我们只要将上一步的数值乘以该二进制数的系数再平方。一直类推下去， 然后把每一步得到的结果res乘起来模上9，就是 3^(1*2^3) * 3^(1*2^2) * 3^(0*2^1) * 3^(1*2^0) (mod 9)

对于所有的a^b (mod n)都可以这么做，把b分解为二进制。这种快速模幂运算也叫蒙哥马利运算。

看代码来理解更方便：

def pow_mod(p, q, n):
    '''
    幂模运算，快速计算(p^q) mod (n)
    这里采用了蒙哥马利算法
    '''
    res = 1
    while q :
        if q & 1: # 如果q & 1=1,那么其二进制形式的最后一位等于1
            res = (res * p) % n
        q >>= 1   # 每一轮右移一位，就能得出其二进制每位是0还是1
        p = (p * p) % n 
    return res

2.产生一个大素数

我们解决的思路是先产生一个大数，然后再判断其是不是素数。

产生大数很简单，直接使用rand函数来产生每一位数字，然后拼接起来不就好了吗。

直接看代码即可

def probin(w):
    '''
    随机产生一个伪素数，产生 w表示希望产生位数
    '''
    list = []
    list.append('1')  #最高位定为1
    for i in range(w - 2):
        c = random.choice(['0', '1'])
        list.append(c)
    list.append('1') # 最低位定为1
    res = int(''.join(list),2)
    return res

通过以上代码我们产生了一个非常大的奇数，但是我们怎么来检验其是否为素数呢，这里使用了非常通用的miller rabin算法来检验。

其算法原理是利用了费马定理的结论：

  • 费马小定理：对于素数p和任意整数a，有a^(p−1) = 1 (mod p)

Miller Rabin素数判定，在费马定理的基础上增加了二次判定：

  • 如果p是素数，则 x^2=1 (mod p)的解为x=1或x=p−1(mod p)

根据费马定理，如果p为素数，正好有 a^(p−1) = 1 (mod p)，那么x^((p-1)/2) = 1 或者 p-1。如果x^((p-1)/2) = 1，那么x^((p-1)/2/2) = 1 或者p-1.....

直到(p-1)/2/2/2/2...不能再继续除2了为止（再除2就会产生小数，这里我们所有的数字都得是整数。）

因为a^(p−1) = 1 (mod p)是必然存在的，那么必然会有一个解。如果直到算到(p-1)除2除不了了也没有结果，那么p就不是素数。

对于任意两个素数都需要符合费马定理，且满足二次定理，即对于任意的a, a^(p−1) = 1 (mod p)有解。

那么满足上述两个条件是否一定证明其为素数，也不是，这只是一个必要但不充分条件，但是科学证明，当取任意多个a都符合上述条件的时候，我们就可以判断其为素数（误判的概率很小）。

接下来我们就来判断一个大数是否满足费马定理和二次定理。

def prime_miller_rabin(a, n): # 随机生成a, 检测n是否为素数
    '''
    第一步，模100以内的素数，初步排除很显然的合数
    '''
    Sushubiao=(2,3,5,7,11,13,17,19,23,29,31,37,41
                ,43,47,53,59,61,67,71,73,79,83,89,97)# 100以内的素数
    for y in Sushubiao:
        if n % y==0:
            return False

    '''
    第二步 用miller rabin算法对n进行检测
    '''
    if pow_mod(a, n-1, n) == 1: # 费马定理，如果a^(n-1)!= 1 mod n, 说明为合数

        d = n-1 # n-1 = (2^q )* m, 求q和m的值，用来判断二次定理
        q = 0
        while not(d & 1):
            q = q+1
            d >>= 1
        m = d

        for i in range(q): # 0~q-1, 我们先找到的最小的a^u，再逐步扩大到a^((n-1)/2)
            u = m * (2**i)  
            tmp = pow_mod(a, u, n)
            if tmp == 1 or tmp == n-1: # 如果满足，则a^(n−1) = 1 (mod n)有解。
                # 满足条件 
                return True
        return False
    else:
        return False

接下来我们随机产生几个a，来检验其是否都满足费马定理和二次定理。

def prime_test(n, k): # 产生k个a
    while k > 0:
        a = random.randint(2, n-1)
        if not prime_miller_rabin(a, n): # 如果返回false，说明这不是个素数，不用继续测试了
            return False
        k = k - 1
    return True

然后就到了产生素数的函数了。这里我们使用while循环，什么时候产生素数成功了什么时候退出。

def get_prime(bit):
    while True:
        prime_number = probin(bit) # 产生bit位的素数
        for i in range(50):  # 伪素数附近50个奇数都没有真素数的话，重新再产生一个伪素数
            u = prime_test(prime_number, 8) # 检验8个a来判断产生的是不是素数
            if u:
                break
            else:
                prime_number = prime_number + 2*(i)
        if u:
            return prime_number
        else:
            continue

上述代码很直观，直接产生一个大奇数来判断，如果不是素数，则把大素数加2再进行判断。依次类推，加上50次以后还不是素数的化则重新生成一个大奇数。

遍历 [奇数, 奇数+100]的范围应该会有一个素数，这样也提高了成功率。

今天上课听老师说还有一种方法来避免盲目的产生大数，设产生大数为A, 如果A对7取模是5，那么A+5、A+12、A+19、A+26都是7的倍数，也就不是素数了，这样就可以排除这些数字。同样的方法对100以内的数字取模，然后排除掉A后的很多数字，下一次就可以直接取没有被排除的数字。这样就需要生成一个数组来保存被排除的数。

其实思路差不多，我的代码是直接加2，实现起来简单一点，如果不需要产生很多很多的大素数，效果应该也不差。

接下来就是RSA了，我们还得取一个e，这里的e是加密用的，如果实现了模幂运算，那么你就会明白e的取值直接影响了加密的速度，一般e的取值都是比较小，几位或者十几位二进制，而且二进制里的1要少（加快模幂运算速度，思考一下为什么）。

e还需要和(p-1)*(q-1)互素，因为要求模幂，这里我们暂定其为65537（二进制为10000000000000001）。如果和(p-1)*(q-1)不互素，那我们就换一个。所以这里还要有个函数来检测e和(p-1)*(q-1)是否互素。

def gcd(a,b):
    '''
    欧几里得算法求最大公约数
    '''
    while a!=0:
        a, b =b%a , a
    return b

代码很简单，利用了欧几里得算法求公约数，公约数为1不就互素了吗。

到现在我们已经确定e和p，q，加密看起来so easy了。

但是解密还要求出解密密钥 d = e ^(-1) (mod (p-1)*(q-1))。这里也就是求e对于(p-1)*(q-1)的逆。

我的天还要实现模逆运算，这里直接网上找了一个，写文章的时候忘记在那里抄的了，对作者说声抱歉！

def mod_1(x, n):
    '''
    扩展欧几里得算法求模逆
    取模负1的算法:计算x2= x^-1 (mod n)的值
    '''
    x0 = x
    y0 = n
    x1 = 0
    y1 = 1
    x2 = 1
    y2 = 0
    while n != 0:
            q = x // n
            (x, n) = (n, x % n)
            (x1, x2) = ((x2 - (q * x1)), x1)
            (y1, y2) = ((y2 - (q * y1)), y1)
    if x2 < 0:
            x2 += y0
    if y2 < 0:
            y2 += x0
    return x2

解密密钥d也算出来了，事情到这里好像就结束了。是的，真的结束了。

好像少了点什么？对，有图才有真相！

result

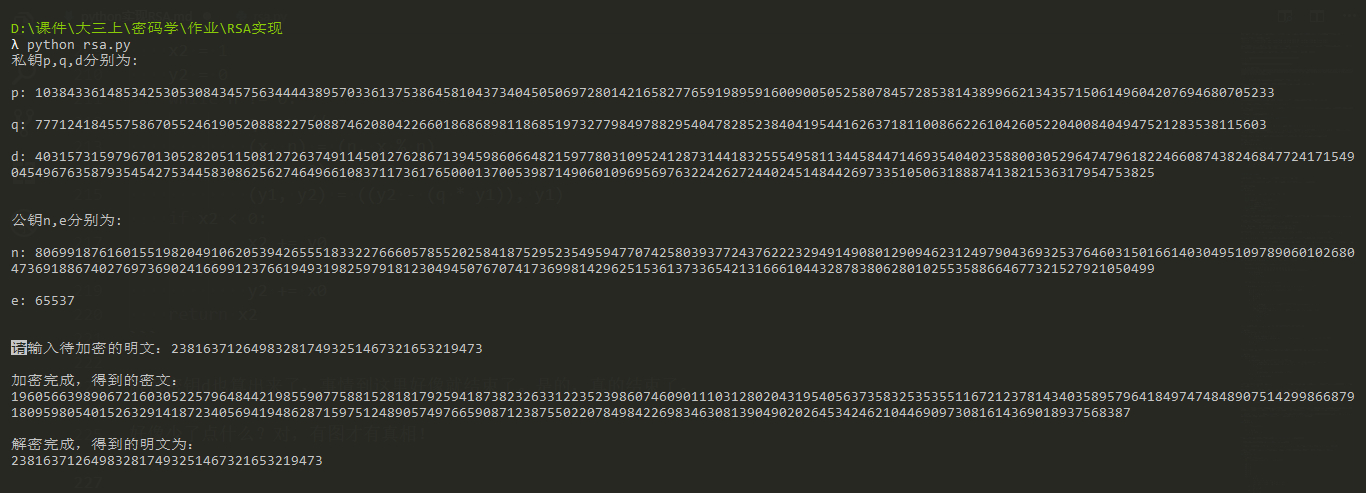
完整的代码已经传到了github上，地址是 https://github.com/saucer-man/rsa

完。

1 + 8 =
4 评论
    小小小张 Chrome 107 Windows 10
    2022年11月24日 回复

    respect

    爱的色放 Chrome 90 Windows 10
    2021年04月29日 回复

    666666

    爱的色放 Chrome 90 Windows 10
    2021年04月29日 回复

    666666

    小菜鸡 Chrome 85 Windows 10
    2020年12月10日 回复

    大佬太强了！